Hypothesis finding with proof theoretical appropriateness criteria
Authors: Bertram Fronhöfer and Akihiro Yamamoto
Source:
Theoretical Computer Science Vol. 350, Issue 1,
January 2006, pp. 140-162
(Special Issue Algorithmic Learning Theory (ALT 2002)).
Abstract.
For two given formulae
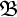and
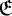with
,
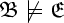hypothesis finding means to produce a formula
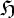such that
∧
⊧ .
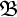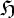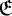Hypothesis finding, or variants thereof, is central to various types of inference,
e.g., abductive inference, inductive inference, machine learning, and machine
discovery. Clarifying the nature of hypothesis finding is still in its infancy,
a situation similar to the establishment of logical foundations of inference related
to induction and discovery. Although trivial solutions to hypothesis finding are
easy to give, finding appropriate hypotheses still remains as a great challenge.
A central role in this context plays the question, what it means for a hypothesis
to be appropriate? In this paper we propose an answer to this question, which is
based on proof theoretical criteria. This is in contrast to most previous
approaches where appropriateness of hypotheses was based on concepts of
semantical weakness in classical logic. More precisely, we use provability
in Relevance Logic instead of classical semantical entailment,
we demand utmost exploitation of the inferential potential
(deductive content) inherent in
→
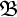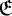and we demand
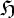to be a minimal deductive
supplement to
→
.
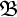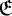Along these lines we developed the concept of a minimized residue hypothesis which
also constitutes an interesting trade-off between ‘logical smallness’
and ‘syntactical smallness’.
Keywords: Hypothesis finding; Connection method; Relevance logic; Residue hypotheses; Inductive logic; Abduction and knowledge discovery