Changing the Inference Type - Keeping the Hypothesis Space Author: Frank Balbach. Source: Lecture Notes in Artificial Intelligence Vol. 2842, 2003, 84 - 98. Abstract. In inductive inference all learning takes place in hypothesis spaces. We investigate for which classes of recursive functions learnability according to an inference type 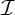implies learnability according to a different inference type within the same hypothesis space. Several classical inference types are considered. Among FIN, CONS-CP, and CP the above implication is true, for all relevant classes, independently from the hypothesis space. On the other hand, it is proved that for many other pairs 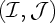hypothesis spaces exist that allow full 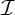learning power, but limit that of to finite classes. Only in a few cases (e.g. LIM vs. CONS) the result does depend on the actual class to be learned. ©Copyright 2003 Springer