Learning a Subclass of Regular Patterns in Polynomial Time
Authors: John Case, Sanjay Jain, Rüdiger Reischuk, Frank Stephan and Thomas Zeugmann.
Source: Lecture Notes in Artificial Intelligence Vol. 2842, 2003, 234 - 246.
Abstract.
Presented is an algorithm (for learning a subclass of erasing regular
pattern languages) which
can be made to run with arbitrarily high probability of
success on extended regular languages generated by patterns
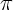of the form
for unknown m but known c,
from number of examples polynomial in m (and exponential in c),
where 
are variables and
where 
are each strings of constants or terminals of
length c. This assumes that the algorithm randomly draws samples
with natural and plausible assumptions on the distribution.
The more general looking case of extended regular patterns which alternate between a variable and fixed length constant strings, beginning and ending with either a variable or a constant string is similarly handled.
©Copyright 2003 Springer