On Ordinal VC-Dimension and Some Notions of Complexity
Authors: Eric Martin, Arun Sharma and Frank Stephan.
Source: Lecture Notes in Artificial Intelligence Vol. 2842, 2003, 54 - 68.
Abstract.
We generalize the classical notion of VC-dimension to
ordinal VC-dimension, in the context of logical learning
paradigms. Logical learning paradigms encompass the
numerical learning paradigms commonly studied in
Inductive inference. A logical learning paradigm is defined
as a set 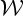 of structures over some vocabulary, and a set
of structures over some vocabulary, and a set 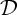 of
first-order formulas that represent data. The sets of
models of
of
first-order formulas that represent data. The sets of
models of 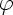 in
in 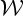 ,
where
,
where 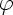 varies over
varies over 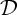 ,
generate a natural
topology W over
,
generate a natural
topology W over 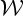 .
.
We show that if 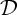 is closed under boolean operators, then the
notion of ordinal VC-dimension offers a perfect
characterization for the problem of predicting the truth of
the members of
is closed under boolean operators, then the
notion of ordinal VC-dimension offers a perfect
characterization for the problem of predicting the truth of
the members of 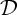 in a member of
in a member of
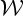 , with an ordinal bound on
the number of mistakes. This shows that the notion of
VC-dimension has a natural interpretation in Inductive
Inference, when cast into a logical setting. We also study
the relationships between predictive complexity, selective
complexity-a variation on predictive complexity-and mind
change complexity. The assumptions that
, with an ordinal bound on
the number of mistakes. This shows that the notion of
VC-dimension has a natural interpretation in Inductive
Inference, when cast into a logical setting. We also study
the relationships between predictive complexity, selective
complexity-a variation on predictive complexity-and mind
change complexity. The assumptions that 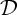 is closed under
boolean operators and that W is compact often play a
crucial role to establish connections between these
concepts.
is closed under
boolean operators and that W is compact often play a
crucial role to establish connections between these
concepts.
Keywords: Inductive inference, logical paradigms, VC-dimension, predictive complexity, mind change bounds.
©Copyright 2003 Springer