A Stochastic Gradient Descent Algorithm for Structural Risk Minimisation Author: Joel Ratsaby. Source: Lecture Notes in Artificial Intelligence Vol. 2842, 2003, 205 - 220. Abstract. Structural risk minimisation (SRM) is a general complexity regularization method which automatically selects the model complexity that approximately minimises the misclassification error probability of the empirical risk minimiser. It does so by adding a complexity penalty term (m,k) to the empirical risk of the candidate hypotheses and then for any fixed sample size m it minimises the sum with respect to the model complexity variable k. When learning multicategory classification there are M subsamples mi, corresponding to the M pattern classes with a priori probabilities pi, 1 i M. Using the usual representation for a multi-category classifier as M individual boolean classifiers, the penalty becomes 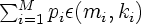. If the mi are given then the standard SRM trivially applies here by minimizing the penalised empirical risk with respect to ki, i = 1, ..., M. However, in situations where the total sample size 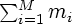needs to be minimal one needs to also minimize the penalised empirical risk with respect to the variables mi, i = 1, ..., M. The obvious problem is that the empirical risk can only be defined after the subsamples (and hence their sizes) are given (known). Utilising an on-line stochastic gradient descent approach, this paper overcomes this difficulty and introduces a sample-querying algorithm which extends the standard SRM principle. It minimises the penalised empirical risk not only with respect to the ki, as the standard SRM does, but also with respect to the mi, i = 1, ..., M. The challenge here is in defining a stochastic empirical criterion which when minimised yields a sequence of subsample-size vectors which asymptotically achieve the Bayes' optimal error convergence rate. ©Copyright 2003 Springer