Efficient Learning of Ordered and Unordered Tree Patterns with Contractible Variables Authors: Yusuke Suzuki, Takayoshi Shoudai, Satoshi Matsumoto, Tomoyuki Uchida and Tetsuhiro Miyahara. Source: Lecture Notes in Artificial Intelligence Vol. 2842, 2003, 114 - 128. Abstract. Due to the rapid growth of tree structured data such as Web documents, efficient learning from tree structured data becomes more and more important. In order to represent structural features common to such tree structured data, we propose a term tree, which is a rooted tree pattern consisting of tree structures and labeled variables. A variable is a labeled hyperedge, which can be replaced with any tree. A contractible variable is an erasing variable which is adjacent to a leaf. A contractible variable may be replaced with a singleton vertex. A usual variable, called an uncontractible variable, is replaced with a tree of size at least 2. In this paper, we deal with ordered and unordered term trees with contractible and uncontractible variables such that all variables have mutually distinct variable labels. First we give a polynomial time algorithm for deciding whether or not a given term tree matches a given tree. Let 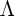be a set of edge labels. Second, when 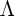has more than one edge label, we give a polynomial time algorithm for finding a minimally generalized ordered term tree which explains all given tree data. 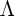Lastly, when has infinitely many edge labels, we give a polynomial time algorithm for finding a minimally generalized unordered term tree which explains all given tree data. These results imply that the classes of ordered and unordered term trees are polynomial time inductively inferable from positive data. ©Copyright 2003 Springer