Learning of Erasing Primitive Formal Systems from Positive Examples Authors: Jin Uemura and Masako Sato. Source: Lecture Notes in Artificial Intelligence Vol. 2842, 2003, 69 - 83. Abstract. An elementary formal system, EFS for short, introduced by Smullyan is a kind of logic program over strings, and is regarded as a grammar to generate a language. Arikawa and his colleagues introduced some subclasses of EFSs which correspond to Chomsky hierarchy, and showed that they constitute a useful framework for language learning. This paper considers a subclass of EFSs, called primitive EFSs, in view of inductive inference in Gold framework from positive examples. Shinohara showed that the class of languages generated by primitive EFSs is inferable from positive examples, where 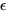substitutions, i.e., substitutions that may substitute the empty string for variables is not allowed. In the present paper, we consider allowing substitutions, and call such EFSs erasing EFSs. It is unknown whether or not the class of erasing pattern languages is learnable from positive examples. An erasing pattern language is a language generated by an erasing EFS with just one axiom. We first show that the class of languages generated by erasing primitive EFSs does not have finite elasticity, but has M-finite thickness. The notions of finite elasticity and M-finite thickness were introduced by Wright, and Moriyama and Sato, respectively, to present sufficient conditions for learnability from positive examples. Moriyama and Sato showed that a language class with M-finite thickness is learnable from positive examples if and only if for each language in the class, there is a finite tell-tale set of the language. Then we show the class is learnable from positive examples by presenting a finite tell-tale set for each language in the class. ©Copyright 2003 Springer