|
Author: Eiji Takimoto
Affiliation:Department of Informatics, Kyushu University
Fukuoka, Japan
Abstract.
We study online linear optimization problems over combinatorial
concept classes
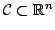 that are
defined in some combinatorial ways.
Examples of such classes are
that are
defined in some combinatorial ways.
Examples of such classes are 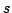 -
- paths in a given
graph, spanning trees of a given graph, permutations over
a given set, truth assignments for a given CNF formula,
set covers of a given subset family, and so on.
Typically, those concept classes are finite but contain
exponentially many concepts.
The problem for a concept class
paths in a given
graph, spanning trees of a given graph, permutations over
a given set, truth assignments for a given CNF formula,
set covers of a given subset family, and so on.
Typically, those concept classes are finite but contain
exponentially many concepts.
The problem for a concept class
 is described
as follows:
At each trial
is described
as follows:
At each trial 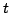 , the algorithm chooses a concept
, the algorithm chooses a concept
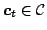 , the adversary returns a loss vector
, the adversary returns a loss vector
![$ \boldsymbol{\ell}_t \in [0,1]^n$](eiji/img6.png) , and the algorithm incurs a loss
given by
, and the algorithm incurs a loss
given by
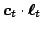 .
The goal of the algorithm is to make the cumulative loss not
much larger than that of the best concept in
.
The goal of the algorithm is to make the cumulative loss not
much larger than that of the best concept in
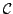 .
.
One of the major approaches to the problem is to apply
Follow the Regularized Leader (FTRL) framework, in which
two external procedures projection and
decomposition are assumed to be implemented.
In other words, for each concept class
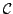 ,
we need to design algorithms for the two procedures.
In this talk, we give a projection and decomposition algorithms
that work efficiently and uniformly for a
wide class of concept classes. More precisely, if the
convex hull of
,
we need to design algorithms for the two procedures.
In this talk, we give a projection and decomposition algorithms
that work efficiently and uniformly for a
wide class of concept classes. More precisely, if the
convex hull of
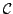 is a
submodular base polyhedron specified by a submodular functoin
is a
submodular base polyhedron specified by a submodular functoin 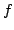 ,
then the two procedures are computed in polynomial time,
assuming that
,
then the two procedures are computed in polynomial time,
assuming that 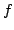 can be computed in polynomial time.
can be computed in polynomial time.
Another approach is to use an offline algorithm as an oracle
to construct an online algorithm.
Here, the offline algorithm solves the corresponding offline
optimization problem.
Follow the perturbed leader (FPL) and the Online Frank-Wolfe (OFW)
are of this type.
In this talk, we consider a harder but typical case where
the offline optimization problem for
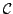 is NP-hard,
for which none of the FTRL, FPL and OFW work.
The FTRL has been generalized so that it works when
an offline approximation algorithm is available.
However, it is not efficient enough.
In this talk, we give a more efficient online algorithm using
an offline approximation algorithm which has a guarantee of
a certain integrity gap.
is NP-hard,
for which none of the FTRL, FPL and OFW work.
The FTRL has been generalized so that it works when
an offline approximation algorithm is available.
However, it is not efficient enough.
In this talk, we give a more efficient online algorithm using
an offline approximation algorithm which has a guarantee of
a certain integrity gap.
©Copyright Author

|