Improved bounds about on-line learning of smooth-functions of a single variable
Author: Philip M. Long.
Email: plong@comp.nus.edu.sg
Source: Theoretical Computer Science Vol. 241,
No. 1-2, 2000, 25-35.
Abstract.
We consider the complexity of learning classes of smooth functions
formed by bounding different norms of a function's derivative. The
learning model is the generalization of the mistake-bound model to
continuous-valued functions. Suppose Fq is the set of all absolutely
continuous functions f from [0,1] to R such that ||f||q 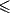 1, and
opt(Fq,m) is
the best possible bound on the worst-case sum of absolute prediction
errors over sequences of m trials. We show that for all q
1, and
opt(Fq,m) is
the best possible bound on the worst-case sum of absolute prediction
errors over sequences of m trials. We show that for all q
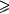 2, opt(Fq,m) =
2, opt(Fq,m) =
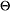 (
(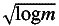 ),
and that opt(F2,m)
),
and that opt(F2,m)
 (
(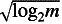 )/2 + O(1), matching a known
lower bound of (
)/2 + O(1), matching a known
lower bound of (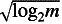 )/2 - O(1) to within an additive constant.
)/2 - O(1) to within an additive constant.
©Copyright 2000 Elsevier Science
 1, and
opt(Fq,m) is
the best possible bound on the worst-case sum of absolute prediction
errors over sequences of m trials. We show that for all q
1, and
opt(Fq,m) is
the best possible bound on the worst-case sum of absolute prediction
errors over sequences of m trials. We show that for all q
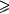 2, opt(Fq,m) =
2, opt(Fq,m) =
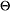 (
(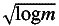 ),
and that opt(F2,m)
),
and that opt(F2,m)
 (
(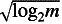 )/2 + O(1), matching a known
lower bound of (
)/2 + O(1), matching a known
lower bound of (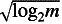 )/2 - O(1) to within an additive constant.
)/2 - O(1) to within an additive constant.