The learnability of exclusive-or expansions ...

The learnability of exclusive-or expansions based on monotone DNF formulas.

Authors: Eiji Takimoto, Yoshifumi Sakai and Akira Maruoka.
Email: t2@eceit.tohoku.ac.jp

Source: Theoretical Computer Science Vol. 241, No. 1-2, 2000, 37-50.

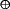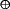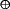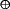Abstract. The learnability of the class of exclusive-or expansions based on monotone DNF formulas is investigated. The class consists of the formulas of the form f = f₁ ^... f_d, where f₁ > ^... > f_d are monotone DNF formulas. It is shown that any Boolean function can be represented as a formula in this class, and that the representation in the simplest form is unique. Learning algorithms that learn such formulas using various queries are presented: An algorithm with subset and superset queries and one with membership and equivalence queries are given. The former can learn any formula in the class, while the latter is proved to learn formulas of constant depth, i.e., formulas represented as exclusive-or of a constant number of monotone DNF formulas. In spite of the seemingly strong restriction of the depth being constant, the class of formulas of constant depth includes functions with very high complexity in terms of DNF and CNF representations, so the latter algorithm could learn Boolean functions significantly complex otherwise represented.