Hierarchies of probabilistic and team FIN-learning
Authors: Andris Ambainis1, Kalvis Apsitis2,
Rusins Freivalds3 and Carl H. Smith4
Email: smith@cs.umd.edu
Source: Theoretical Computer Science Vol. 261, Issue 1, 17 June 2001, pp. 91-117.
Abstract.
A FIN-learning machine M receives successive values of the function
f it is learning and at some moment outputs a conjecture which should
be a correct index of f. FIN learning has two extensions:
(1) If M flips fair coins and learns a function
with certain probability p, we have FIN<p>-learning.
(2) When n machines simultaneously try to learn the same function f and at least k of these machines output correct indices
of f, we have learning by a [k,n]FIN team. Sometimes a team
or a probabilistic learner can simulate another one, if their probabilities
p1, p2 (or team success ratios
k1/n1, k2/n2)
re close enough (Daley et al., in: Valiant, Waranth (Eds.),
Proc. 5th Annual Workshop on Computational Learning Theory, ACM
Press, New York, 1992, pp. 203-217; Daley and Kalyanasundaram, Available from
http://www.cs.pitt.edu/daley/fin/fin.html, 1996). On the other hand, there are
cut-points r which make simulation of FIN<p2>
by FIN<p1> impossible whenever p2
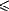 r < p1.
Cut-points above 10/21 are known (Daley and Kalyanasundaram,
Available from http://www.cs.pitt.edu/~daley/fin/fin.html, 1996). We show that
the problem for given ki, ni
to determine whether [k1,n1]FIN
r < p1.
Cut-points above 10/21 are known (Daley and Kalyanasundaram,
Available from http://www.cs.pitt.edu/~daley/fin/fin.html, 1996). We show that
the problem for given ki, ni
to determine whether [k1,n1]FIN
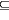 [k2,n2]FIN
is algorithmically solvable. The set of all FIN cut-points is shown to be well
ordered and recursive. Asymmetric teams are introduced and used as both a tool
to obtain these results, and are of interest in themselves. The framework of
asymmetric teams allows us to characterize intersections
[k1,n1]FIN
[k2,n2]FIN
is algorithmically solvable. The set of all FIN cut-points is shown to be well
ordered and recursive. Asymmetric teams are introduced and used as both a tool
to obtain these results, and are of interest in themselves. The framework of
asymmetric teams allows us to characterize intersections
[k1,n1]FIN
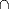 [k2,n2]FIN, unions
[k1,n1]FIN
[k2,n2]FIN, unions
[k1,n1]FIN
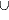 [k2,n2]FIN,
and memberwise unions
[k1,n1]FIN +
[k2,n2]FIN, i.e.,
collections of all unions U1
[k2,n2]FIN,
and memberwise unions
[k1,n1]FIN +
[k2,n2]FIN, i.e.,
collections of all unions U1
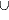 U2 where Ui
U2 where Ui
 [ki,ni]FIN.
Hence, we can compare the
learning power of traditional FIN-teams [k,n]FIN as well as all
kinds of their set-theoretic combinations.
[ki,ni]FIN.
Hence, we can compare the
learning power of traditional FIN-teams [k,n]FIN as well as all
kinds of their set-theoretic combinations.
1Part of this work done at the University of Latvia, supported by Latvia Science Council Grant 98.0282.
2Part of this work done at the University of Maryland.
3Supported by Latvia Science Council Grant 96.0282.
4Supported in part by National Science Foundation Grant CCR-9732692.