Aspects of complexity of probabilistic learning under monotonicity constraints
Author: Léa Meyer
Email: lea@modell.iig.uni-freiburg.de
Source: Theoretical Computer Science Vol. 268, Issue 2, 17 October 2001, pp. 275 - 322.
Abstract.
In the setting of learning indexed families, probabilistic learning under
monotonicity constraints is more powerful than deterministic learning under
monotonicity constraints, even if the probability is close to 1, provided the
learning machines are restricted to proper or class preserving hypothesis spaces
(cf. Meyer, Theoret. Comput. Sci. 185 (1997) 81-128). In this paper, we
investigate the relation between probabilistic learning and oracle identification
under monotonicity constraints. In particular, we deal with the question how
much additional information provided by oracles is necessary for compensating
the additional power of probabilistic learning
machines. In Section 1, we show that K is necessary and sufficient to
compensate the additional power of probabilistic learning machines in the case
of conservative (monotonic) probabilistic learning with
p > 1/2 (2/3), and for strong-monotonic probabilistic learning with
1/2 < p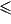 
2/3.
In the case of strong-monotonic learning with p > 2/3, however,
every Peano-complete oracle is sufficient for compensating the
power of probabilistic learning machines. In contrast, the oracle K
is not sufficient for compensating the power of conservative and
strong-monotonic probabilistic learning with probability
p = 1/2, and monotonic probabilistic learning with p = 2/3.
The main result in Section 2 is that for each oracle A
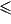T
K, there exists an indexed family
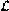A
which is monotonically learnable with probability p = 1/2, and which
exactly reflects the Turing degree of A, i.e.,
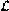A
is properly conservatively identifiable by an oracle machine M[B]
iff A
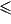T
B.
Thus, for every oracle A below K, we can construct a learning
problem characterizing A within proper conservative learning.
However, not every indexed family which is conservatively identifiable with
probability p = 1/2 reflects the Turing degree of an oracle. Hence,
the conservative probabilistic learning classes are higher structured than the
Turing degrees below K.
Finally, we prove that there exist learning problems which are conservatively
(monotonically) identifiable with probability p = 1/2 (p = 2/3),
but conservatively
(monotonically) identifiable only by oracle machines having access to TOT.
For strong-monotonic learning, this result does not hold.