Learning algebraic structures from text*
Authors: Frank Stephan and Yuri Ventsov
Email: fstephan@math.uni-heidelberg.de
Source: Theoretical Computer Science Vol. 268, Issue 2, 17 October 2001, pp. 221 - 273.
Abstract. The present work investigates the learnability of classes of substructures of some algebraic structures: submonoids and subgroups of given groups, ideals of given commutative rings, subfields of given vector spaces. The learner sees all positive data but no negative one and converges to a program enumerating or computing the set to be learned. Besides semantical (BC) and syntactical (Ex) convergence also the more restrictive ordinal bounds on the number of mind changes are considered. The following is shown: (a) Learnability depends much on the amount of semantic knowledge given at the synthesis of the learner where this knowledge is represented by programs for the algebraic operations, codes for prominent elements of the algebraic structure (like 0 and 1 fields) and certain parameters (like the dimension of finite-dimensional vector spaces). For several natural examples, good knowledge of the semantics may enable to keep ordinal mind change bounds while restricted knowledge may either allow only BC-convergence or even not permit learnability at all.
(b) The class of all ideals of a recursive ring is BC-learnable iff the ring is
Noetherian. Furthermore, one has either only a BC-learner outputting enumerable
indices or one can already get an Ex-learner converging to decision procedures
and respecting an ordinal bound on the number of mind changes. The ring is
Artinian iff the ideals can be Ex-learned with a constant bound on the number
of mind changes, this constant is the length of the ring. Ex-learnability
depends not only on the ring but also on the representation of the ring.
Polynomial rings over the field of rationals
with n variables have exactly the ordinal mind change bound
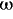 n
in the standard
representation. Similar results can be established for unars.
Noetherian unars with
one function can be learned with an ordinal mind change bound
a
n
in the standard
representation. Similar results can be established for unars.
Noetherian unars with
one function can be learned with an ordinal mind change bound
a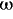 for some
a.
for some
a.
* An abstract of this paper appeared at the proceedings of the Ninth International Conference on Algorithmic Learning Theory 1998 in Kaiserslautern. This paper was written when Frank Stephan was visiting Arun Sharma at the School of Computer Science and Engineering, UNSW. The first author is supported by the Deutsche Forschungsgemeinschaft (DFG) grant Am 60/9-2. The second author is supported by the Australian Research Council grant A49600456 to Arun Sharma. The latter grant also supported the first author's visit to UNSW.