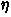PAC Learning with Nasty Noise

Authors: Nader H. Bshouty, Nadav Eiron and Eyal Kushilevitz.

Source: Lecture Notes in Artificial Intelligence Vol. 1720, 1999, 206 - 218.

Abstract. We introduce a new model for learning in the presence of noise, which we call the Nasty Noise model. This model generalizes previously considered models of learning with noise. The learning process in this model, which is a variant of the PAC model, proceeds as follows: Suppose that the learning algorithm during its execution asks for m examples. The examples that the algorithm gets are generated by a nasty adversary that works according to the following steps. First, the adversary chooses m examples (independently) according to the fixed (but unknown to the learning algorithm) distribution D as in the PAC-model. Then the powerful adversary, upon seeing the specific m examples that were chosen (and using his knowledge of the target function, the distribution D and the learning algorithm), is allowed to remove a fraction of the examples at its choice, and replace these examples by the same number of arbitrary examples of its choice; the m modified examples are then given to the learning algorithm. The only restriction on the adversary is that the number of examples that the adversary is allowed to modify should be distributed according to a binomial distribution with parameters 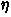(the noise rate) and m.

On the negative side, we prove that no algorithm can achieve accuracy of < 2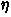 in learning any non-trivial class of functions. On the positive side, we show that a polynomial (in the usual parameters, and in - 2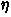) number of examples suffice for learning any class of finite VC-dimension with accuracy > 2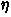. This algorithm may not be efficient; however, we also show that a fairly wide family of concept classes can be efficiently learned in the presence of nasty noise.