Proper learning algorithm for functions of k
terms under smooth distributions
Authors: Yoshifumi Sakai, Eiji Takimoto, and Akira Maruoka
Source: Information & Computation Vol. 152, No. 2,
1999, 188 - 204.
Abstract.
In this paper, we introduce a probabilistic distribution, called a smooth
distribution, which is a generalization of variants of the uniform distribution
such as q-bounded distribution and product distribution.
Then, we give an algorithm that, under the smooth distribution, properly learns
the class of functions of k terms given as
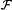 k
k
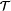 kn={g(f1(v),...,fk(v)) | g
kn={g(f1(v),...,fk(v)) | g 
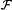 k,
fv,..., fk
k,
fv,..., fk
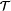 n}
in polynomial time for constant k, where
n}
in polynomial time for constant k, where 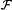 k
is the class of all Boolean functions of k variables and
k
is the class of all Boolean functions of k variables and
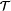 n is the class of terms over
n variables. Although class
n is the class of terms over
n variables. Although class
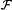 k
k
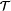 kn was shown by Blum and Singh to be learned using DNF as the hypothesis class, it has remained open whether it
is properly learnable under a distribution-free setting.
kn was shown by Blum and Singh to be learned using DNF as the hypothesis class, it has remained open whether it
is properly learnable under a distribution-free setting.
©Copyright 1999, Academic Press
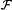 k
k
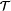 kn={g(f1(v),...,fk(v)) | g
kn={g(f1(v),...,fk(v)) | g 
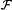 k,
fv,..., fk
k,
fv,..., fk
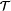 n}
in polynomial time for constant k, where
n}
in polynomial time for constant k, where 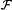 k
is the class of all Boolean functions of k variables and
k
is the class of all Boolean functions of k variables and
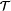 n is the class of terms over
n variables. Although class
n is the class of terms over
n variables. Although class
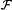 k
k
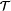 kn was shown by Blum and Singh to be learned using DNF as the hypothesis class, it has remained open whether it
is properly learnable under a distribution-free setting.
kn was shown by Blum and Singh to be learned using DNF as the hypothesis class, it has remained open whether it
is properly learnable under a distribution-free setting.