Co-Learning of Recursive Languages from Positive Data
Authors: Rusins Freivalds and Thomas Zeugmann
Source: Perspectives of System Informatics,
Second International Andrei Ershov Memorial Conference, Akademgorodok,
Novosibirsk, Russia, June 1996, Proceedings,
(D. Bjørner, M. Broy, and I. Pottosin, Eds.),
Lecture Notes in
Computer Science 1181, pp. 122 - 133, Springer 1996.
Abstract.
The present paper deals with the co-learnability of enumerable families
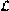 of uniformly recursive languages from positive data.
This refers to
the following scenario. A family
of uniformly recursive languages from positive data.
This refers to
the following scenario. A family 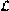 of target languages as well as
hypothesis space for it are specified. The co-learner is fed
eventually all positive examples of an unknown target language L chosen
from
of target languages as well as
hypothesis space for it are specified. The co-learner is fed
eventually all positive examples of an unknown target language L chosen
from 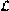 . The target language L is successfully co-learned iff the
co-learner can definitely delete all but one possible hypotheses, and the
remaining one has to correctly describe L.
. The target language L is successfully co-learned iff the
co-learner can definitely delete all but one possible hypotheses, and the
remaining one has to correctly describe L.
The capabilities of co-learning are investigated in dependence on the
choice of
the hypothesis space, and compared to language learning in the limit,
conservative learning and finite learning from positive
data.
Class preserving learning (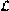 has to be co-learned with
respect to some suitably chosen enumeration of all and only the languages
from
has to be co-learned with
respect to some suitably chosen enumeration of all and only the languages
from 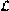 ), class comprising learning (
), class comprising learning (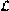 has to be co-learned
with respect to some hypothesis space containing at least all the languages
from
has to be co-learned
with respect to some hypothesis space containing at least all the languages
from 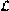 ), and absolute co-learning (
), and absolute co-learning (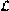 has to be co-learned
with respect to all class preserving hypothesis spaces for
has to be co-learned
with respect to all class preserving hypothesis spaces for  )
are distinguished.
\par
Our results are manyfold. First, it is shown that co-learning is exactly as powerful
as learning in the limit provided the hypothesis space is appropriately chosen.
However, while learning in the limit is insensitive to the particular
choice of the hypothesis space, the power of co-learning crucially depends on it.
Therefore the properties a hypothesis space should have in order
to be suitable for co-learning are studied. Finally, a sufficient conditions for
absolute co-learnability is derived, and it is separated from finite learning.
)
are distinguished.
\par
Our results are manyfold. First, it is shown that co-learning is exactly as powerful
as learning in the limit provided the hypothesis space is appropriately chosen.
However, while learning in the limit is insensitive to the particular
choice of the hypothesis space, the power of co-learning crucially depends on it.
Therefore the properties a hypothesis space should have in order
to be suitable for co-learning are studied. Finally, a sufficient conditions for
absolute co-learnability is derived, and it is separated from finite learning.
©Copyright 1996, Springer-Verlag.