Theory of Computation
by Thomas Zeugmann, Sin-ichi Minato, and Yoshiaki Okubo
Table of Contents
1.   Introducing Formal Languages
1.1   Introduction	1
1.2   Basic Definitions and Notations	2
1.3   Strings and Languages	7
1.4   Palindromes	9
1.5   Problem Set 1	13
2.   Introducing Formal Grammars
2.1   Defining Formal Grammars	14
2.2   Regular Languages	16
2.3   Problem Set 2	20
3.   Finite State Automata
3.1   Computing with Finite Automata 22
3.2   Finite Automata and Regular Languages	25
3.3   Problem Set 3	30
4.   Characterizations of REG
4.1   Nerode’s Theorem	31
4.2   Regular Expressions	33
4.3   The Pumping Lemma for Regular Languages	37
4.4   Problem Set 4	40
5.   Regular Expressions in UNIX
5.1   Lexical Analysis.	43
5.2   Finding Patterns in Text	45
5.3   Problem Set 5	47
6.   Context-Free Languages
6.1   Defining Context-Free Languages	48
6.2   Closure Properties for Context-Free Languages	49
6.3   Problem Set 6	58
7.   More About Context-Free Languages
7.1   Backus-Naur Form	59
7.2   Parse Trees, Ambiguity	61
7.3   Chomsky Normal Form	69
7.4   Problem Set 7	75
8.   CF and Homomorphisms
8.1   Substitutions and Homomorphisms	76
8.2   Homomorphic Characterization of CF	82
8.3   Problem Set 8	91
9.   Pushdown Automata
9.1   Introducing Pushdown Automata	92
9.2   PDAs and Context-Free Languages	100
9.3   Problem Set 9	104
10.   CF, PDAs and Beyond
10.1   Greibach Normal Form	105
10.2   Main Theorem	111
10.3   Context-Sensitive Languages	114
10.4   Problem Set 10	117
11.   Models of Computation
11.1   Partial Recursive Functions	121
11.2   Pairing Functions	131
11.3   General Recursive Functions	133
11.4   Problem Set 11	136
12.   Turing Machines
12.1   One-tape Turing Machines	137
12.2   Turing Computations	139
12.3   The Universal Turing Machine	146
12.4   Accepting Languages	150
12.5   Problem Set 12	152
13.   Algorithmic Unsolvability
13.1   The Halting Problem	153
13.2   Post’s Correspondence Problem	156
13.3   Problem Set 13	167
14.   Applications of PCP
14.1   Results for Context-Free Languages	168
14.2   Back to Regular Languages	174
14.3   Results concerning	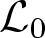175
14.4   Summary	180
14.5   Problem Set 14	181
15.   Numberings, Complexity
15.1   Gödel Numberings	183
15.2   The Fixed Point, the Recursion, and Rice’s Theorems	184
15.3   Complexity	188
15.4   Complexity Classes	195
15.4.1   Recursive Enumerability of Complexity Classes	197
15.4.2   An Undecidability Result	202
15.4.3   The Gap-Theorem	204
15.5   Problem Set 15	206
Appendix
A.1   Greek Alphabet（ギリシャ文字）	207
Bibliography	208
Subject Index	211
和 英 索 引	217
List of Symbols	221
16.   Solutions of Problems
Chapter 16 is on the CD-ROM, see chapter16.pdf
16.1   Solving Problem Set 1	223
16.2   Solving Problem Set 2	226
16.3   Solving Problem Set 3	231
16.4   Solving Problem Set 4	237
16.5   Solving Problem Set 5	241
16.6   Solving Problem Set 6	247
16.7   Solving Problem Set 7	254
16.8   Solving Problem Set 8	257
16.9   Solving Problem Set 9	261
16.10   Solving Problem Set 10	265
16.11   Solving Problem Set 11	270
16.12   Solving Problem Set 12	275
16.13   Solving Problem Set 13	278
16.14   Solving Problem Set 14	282
16.15   Solving Problem Set 15	285

---