On Learning Correlated Boolean Functions Using Statistical Queries (Extended Abstract) Author: Ke Yang. Source: Lecture Notes in Artificial Intelligence Vol. 2225, 2001, 59 - 76. Abstract. In this paper, we study the problem of using statistical query (SQ) to learn a class of highly correlated boolean functions, namely, a class of functions where any pair agree on significantly more than 1/2 fraction of the inputs. We give an almost-tight bound on how well one can approximate all the functions without making any query, and then we show that beyond this bound, the number of statistical queries the algorithm has to make increases with the ``extra'' advantage the algorithm gains in learning the functions. Here the advantage is defined to be the probability the algorithm agrees with the target function minus the probability the algorithm doesn't agree. 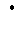An interesting consequence of our results is that the class of booleanized linear functions over a finite field (f(a(x) = 1 iff (ax) = 1, where is an arbitrary boolean function that maps any elements in GFp to 1) is not efficiently learnable. This result is useful since the hardness of learning booleanized linear functions over a finite field is related to the security of certain cryptosystems ([B01]). 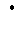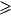In particular, we prove that the class of linear threshold functions over a finite field (f(a,b(x) = 1 iff ax b) cannot be learned efficiently using statistical query. This contrasts with Blum et. al.'s result [BFK+96] that linear threshold functions over reals (perceptions) are learnable using the SQ model. Finally, we describe a PAC-learning algorithm that learns a class of linear threshold functions in time that is provably impossible for statistical query algorithms. With properly chosen parameters, this class of linear threshold functions become an example of PAC-learnable, but not SQ-learnable functions that are not parity functions. ©Copyright 2001 Springer