Reconstructing Weighted Graphs with Minimal Query Complexity

Authors: Nader H. Bshouty and Hanna Mazzawi

Source: Algorithmic Learning Theory, 20th International Conference, ALT 2009, Porto, Portugal, October 2009, Proceedings,
Lecture Notes in Artificial Intelligence 5809, pp. 97 – 109, Springer, 2009.

Abstract. In this paper we consider the problem of reconstructing a hidden weighted graph using additive queries. We prove the following: Let G be a weighted hidden graph with n vertices and m edges such that the weights on the edges are bounded between n^–a and n^b for any positive constants a and b. For any m there exists a non-adaptive algorithm that finds the edges of the graph using

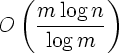
$O\left(\frac{m\log n}{\log m}\right)$
additive queries. This solves the open problem in [S. Choi, J. H. Kim. Optimal Query Complexity Bounds for Finding Graphs. Proc. of the 40th annual ACM Symposium on Theory of Computing , 749–758, 2008]. Choi and Kim’s proof holds for m ≥ (log n)^α for a sufficiently large constant α and uses graph theory. We use the algebraic approach for the problem. Our proof is simple and holds for any m.

The slides of the talk presented at ALT 2009 are available.