Toward a Classification of Finite Partial-Monitoring Games

Authors: Gábor Bartók, Dávid Pál, and Csaba Szepesvári

Source: Algorithmic Learning Theory, 21st International Conference, ALT 2010, Canberra, Australia, October 6 - 8, 2010, Proceedings.
Lecture Notes in Artificial Intelligence 6331, pp. 224 - 238, Springer, 2010.

Abstract. In a finite partial-monitoring game against Nature, the Learner repeatedly chooses one of finitely many actions, the Nature responds with one of finitely many outcomes, the Learner suffers a loss and receives feedback signal, both of which are fixed functions of the action and the outcome. The goal of the Learner is to minimize its total cumulative loss. We make progress towards classifcation of these games based on their minimax expected regret. Namely, we classify almost all games with two outcomes: We show that their minimax expected regret is either zero, 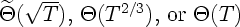$\widetilde{\Theta}(\sqrt{T})$, $\Theta(T^{2/3})$, or $\Theta(T)$ and we give a simple and efficiently computable classification of these four classes of games. Our hope is that the result can serve as a stepping stone toward classifying all finite partial-monitoring games.