Optimal Online Prediction in Adversarial Environments
(invited lecture for ALT & DS 2010)
Author: Peter L. Bartlett
Affiliation:
Computer Science Division and Department of Statistics
University of California at Berkeley, Berkeley CA 94720, USA.
Abstract.
In many prediction problems, including those that
arise in computer security and computational finance,
the process generating the data is best modelled as an
adversary with whom the predictor competes.
Even decision problems that are
not inherently adversarial can be usefully modeled in
this way, since the assumptions are sufficiently weak that
effective prediction strategies for adversarial settings
are very widely applicable.
The first
part of the talk is concerned with the regret of an optimal
strategy for a general online repeated decision problem:
At round t, the strategy chooses an action (possibly random)
at from a set 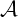 , then the
world reveals a function , then the
world reveals a function 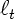 from a set from a set 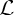 , and the
strategy incurs a loss , and the
strategy incurs a loss 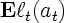 .
The aim of the strategy
is to ensure that the regret, that is, .
The aim of the strategy
is to ensure that the regret, that is,
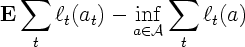
is small.
The results we present [1] are
closely related to finite sample analyses of prediction
strategies for probabilistic settings, where the data
are chosen iid from an unknown probability distribution.
In particular, we relate the
optimal regret to a measure of complexity of the comparison
class that is a generalization of the Rademacher averages that
have been studied in the iid setting.
Many learning problems
can be cast as online convex optimization,
a special case of online repeated decision problems in which
the action set 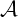 and the
loss functions and the
loss functions 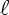 are convex.
The second part of the talk considers optimal strategies for
online convex optimization [2,3].
We present the explicit minimax strategy for several games of this kind,
under a variety of constraints on the convexity of the loss functions
and the action set are convex.
The second part of the talk considers optimal strategies for
online convex optimization [2,3].
We present the explicit minimax strategy for several games of this kind,
under a variety of constraints on the convexity of the loss functions
and the action set 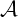 . The key factor is the
convexity of the loss functions: curved loss
functions make the decision problem easier. We also
demonstrate a strategy that can adapt to the difficulty of the game,
that is, the strength of the convexity of the loss functions, achieving
almost the same regret that would be possible if the strategy had
known this in advance. . The key factor is the
convexity of the loss functions: curved loss
functions make the decision problem easier. We also
demonstrate a strategy that can adapt to the difficulty of the game,
that is, the strength of the convexity of the loss functions, achieving
almost the same regret that would be possible if the strategy had
known this in advance.
References
[1] Abernethy, J., Agarwal, A., Bartlett, P.~L., Rakhlin, A.:
A stochastic view of optimal regret through minimax duality.
arXiv:0903.5328v1 [cs.LG] (2009)
[2] Abernethy, J., Bartlett, P.~L., Rakhlin, A., Tewari, A.:
Optimal strategies and minimax lower bounds for online convex games.
UC Berkeley EECS Technical Report EECS-2008-19 (2008)
[3] Bartlett, P.~L., Hazan, E., Rakhlin, A.:
Adaptive online gradient descent.
UC Berkeley EECS Technical Report EECS-2007-82 (2007)
©Copyright 2010 Springer

|