Comparing the Power of Probabilistic Learning and Oracle Identification under Monotonicity Constraints Author: Léa Meyer Source: Lecture Notes in Artificial Intelligence Vol. 1501, 1998, 306 - 320. Abstract. In the setting of learning indexed families, probabilistic learning under monotonicity constraints is more powerful than deterministic learning under monotonicity constraints even if the probability is close to 1 provided the learning machines are restricted to proper or class preserving hypothesis spaces (cf. [19]). In this paper, we investigate the relation between probabilistic learning and oracle identification under monotonicity constraints. In particular, we deal with the question how much ``additional information'' provided by oracles is necessary in order to compensate the additional power of probabilistic learning. If the oracle machines have access to K-oracle, then they can compensate the power of monotonic (conservative) probabilistic machines completely, provided the probability p is greater than 2/3 (1/2). Furthermore, we show that for every recursively enumerable oracle A, there exists a learning problem which is strong-monotonically learnable by an oracle machine having access to A, but not conservatively or monotonically learnable with any probability p > 0. A similar result holds for Peano-complete oracles. However, probabilistic learning under monotonicity constraints is ``rich'' enough to encode every recursively enumerable set in a characteristic learning problem, i.e., for every recursively enumerable set A, and every p > 2/3, there exists a learning problem 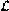A which is monotonically learnable with probability p, and monotonically learnable with oracle B if and only if A is Turing-reducible to B. The same result holds for conservative probabilistic learning with p >1/2, and strong-monotonic learning with probability p =2/3. In particular, it follows that probabilistic learning under monotonicity constraints cannot be characterized in terms of oracle identification. Moreover, we close an open problem that appeared in [19] by showing that the probabilistic hierarchies of class preserving monotonic and conservative probabilistic learning are dense. Finally, we show that these probability bounds are strict, i.e., in the case of monotonic probabilistic learning with probability p = 2/3, conservative probabilistic learning with probability p = 1/2, and strong-monotonic probabilistic learning with probability p = 1/2, K is not sufficient to compensate the power of probabilistic learning under monotonicity constraints. ©Copyright 1998 Springer