Characteristic Sets for Unions of Regular Pattern Languages and Compactness Authors: Masako Sato, Yasuhito Mukouchi, and Dao Zheng Source: Lecture Notes in Artificial Intelligence Vol. 1501, 1998, 220 -233. Abstract. The paper deals with the class 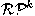of sets of at most k regular patterns. A semantics of a set P of regular patterns is a union L(P) of languages defined by patterns in P. 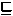A set Q of regular patterns is said to be a more general than P, denoted by P Q, if for any p P, there is a more general pattern q in Q than p. It is known that the syntactic containment P 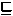Q for sets of regular patterns is efficiently computable. We prove that for any sets P and Q in 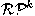, (i) S2(P) 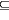L(Q), (ii) the syntactic containment P 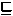Q and (iii) the semantic containment L(P) 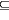L(Q) are equivalent mutually, provided 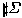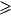2k - 1$, where Sn(P) is the set of strings obtained from P by substituting strings with length at most n for each variable. The result means that S2(P) is a characteristic set of L(P) within the language class for 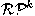under the condition above. Arimura et al. showed that the class 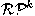has compactness with respect to containment, if 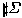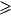2k + 1$. 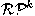By the equivalency above, we prove that has compactness if and only if 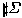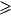2k - 1$. The results obtained enable us to design efficient learning algorithms of unions of regular pattern languages such as already presented by Arimura et al. under the assumption of compactness. ©Copyright 1998 Springer