Abstract.
Presented is an algorithm (for learning a subclass of erasing regular
pattern languages) which
can be made to run with arbitrarily high probability of
success on extended regular languages generated by patterns
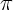of the form
for unknown m but known c,
from number of examples polynomial in m (and exponential in c),
where 
are variables and
where 
are each strings of constants or terminals of
length c. This assumes that the algorithm randomly draws samples
with natural and plausible assumptions on the distribution.
With the aim of finding a better algorithm, we also explore computer
simulations of a heuristic.
* Supported in part by NSF grant number CCR-0208616 and USDA IFAFS grant number 01-04145
** Supported in part by NUS grant number R252-000-127-112.
*** National ICT Australia is funded by the Australian Government's Department of Communications, Information Technology and the Arts and the Australian Research Council through Backing Australia's Ability and the ICT Centre of Excellence Program.