Set-Driven and Rearrangement-Independent Learning of Recursive Languages

Author: Steffen Lange and Thomas Zeugmann

Source: Mathematical Systems Theory 29, No. 6, 1996, 599 - 634.

Abstract. The present paper studies the impact of order independence to the learnability of indexed families 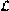of uniformly recursive languages from positive data. In particular, we consider set-driven and rearrangement-independent learners, i.e., learning devices whose output exclusively depends on the range and on the range and length of their input, respectively. The impact of set-drivenness and rearrangement-independence on the behavior of learners to their learning power is studied in dependence on the hypothesis space the learners may use. 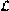We distinguish between exact learnability ( has to be inferred with respect to 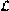), class preserving learning ( 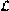has to be inferred with respect to some suitably chosen enumeration of all the languages from 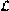), and class comprising inference (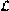 has to be learned with respect to some suitably chosen enumeration of uniformly recursive languages containing at least all the languages from ).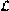

Furthermore, we consider the influence of set-drivenness and rearrangement-independence for learning devices that realize the subset principle to different extents. Thereby we distinguish between strong-monotonic, monotonic and weak-monotonic or conservative learning.

The results obtained are threefold. First, rearrangement-independent learning does not constitute a restriction except the case of monotonic learning. Next, we prove that for all but two of the considered learning models set-drivenness is a severe restriction. However, class comprising set-driven conservative learning is exactly as powerful as unrestricted class comprising conservative learning. Finally, the power of class comprising set-driven learning in the limit is characterized by equating the collection of learnable indexed families with the collection of class comprisingly conservatively inferable indexed families. These results considerably extend previous work done in the field (cf., e.g., Schäfer-Richter (1984) and Fulk (1990)).